| |
|
 |
|
|
在前面章節介紹了,如何利用個體-關係模式(E-R Model)
來建立關聯式資料庫。但是並不是每一個利用個體關係模式建立的關聯式資料表格都是良好設計的關聯表。有時候,不良設計的關聯表在做資料的新增、刪除或更新時,會造成前面介紹的異常現象(Anomalies),所以良好的關聯表中含有最少量的重覆狀況,並可以讓使用者新增、刪除或更新關聯表中的資料,而不會發生資料錯誤或不一致的情況。
|
 |
|
|
在正式介紹正規化(Normalization)
的方法之前,先介紹以下的名詞:
|
 |
鍵值屬性
(Key Attribute) |
候選鍵的組成屬性,稱為鍵值屬性;否則稱為非鍵值屬性(Non-Key Attribute)。 |
 |
部份功能相依
(Partial Furctional
Dependence) |
假設 X→Y,若 H
為 X 的部份屬性 (也就是 H 包含於 X 中) 使得 H→Y 稱之 Y 部份功能相依於 X;否則稱之 Y
完全功能相依於 X。 |
 |
遞移相依
(Transitive
Dependency) |
假設
X→Y,若存在一個非鍵值屬性子集合 Z,使得 X→Z 且 Z→Y 的功能相依性均成立,則稱之 Y 遞移相依於 X。 |
|
|
假設我們有一學生選課資料表格 SC,其中包括學生學號(Sno)、課程代號(Cno)、課程名稱(Cname)、學分數(Credit) 與成績(Score): |
|
|
|
Sno
|
Cno
|
Cname
|
Credit
|
Score
|
|
S1879032
|
Math1416
|
工程數學(一)
|
3
|
60
|
|
S1879044
|
Math1416
|
工程數學(一)
|
3
|
80
|
|
S1882032
|
Cs1318
|
計算機概論
|
4
|
58
|
|
S1879044
|
Cs1318
|
計算機概論
|
4
|
80
|
|
…
|
…
|
…
|
…
|
…
|
|
S1879032
|
Cs1446
|
資料庫
|
2
|
65
|
圖 1 學生選課表格 SC |
|
其中主鍵為( Sno, Cno)而且其表格內的功能相依性如下:
(Sno, Cno) → Score
Cno →Cname
Cno → Credit
|
|
(1)
假設學校下學期有新開一個 3 學分課程 網路概論
Cs1666。因為是新課程,所以沒有學生選修,當然也沒有分數,因此學生學號與成績都為虛值(Null)。如果我們強制將這新的課程 Cs1666
加入表格 SC 中
|
|
|
|
便會使得主鍵(Sno, Cno) 中的 Sno 為虛值了,如此違反了關聯式資料模式中所規定的個體整合限制規則(Entity
Integrity Rules)。這種因新增時違反了“主鍵值不可以為虛值”的限制規則,因而無法新增資料到表格中的現象,稱為新增異常(Insert
Anomalies)。
|
|
(2)
假設只有 S1883035 同學修 Cs2324 程式設計,而後 S1883035
同學退選,因此必須刪除這一筆記錄。
|
|
S1883035
|
Cs2324
|
程式設計
|
3
|
Null
|
|
|
由於原先只有一位同學選修 Cs2324,所以資料表格中,只有一筆 Cs2324 的資料,因此刪除這一筆記錄時,會使 Cs2324 課程為 3
學分的課程資訊也一併被刪除了。因此造成 Cs2324 課程的資訊的遺失,這種因刪除時,連帶刪除了有用資料的情況,稱為刪除異常(Deletion
Anomalies)。
|
|
(3)
假設因工程數學(一)課程的課程名稱更改為微積分,因此必須更改Math1416 的課程名稱。因為
Math1416 可能有多位同學選修,因此必須將表格中所有的 Math1416 的課程名稱做更改,萬一不小心只更改了部份 Math1416
記錄的課程名稱時,便會造成資料的不一致的情況。這種因資料的重覆,因而在更新時必須更改多筆以上的記錄,否則會產生不一致的情況,稱為更新異常(Modification
Anomalies)。
上述的例子說明一點,因為表格設計不良,會造成新增、刪除與更新時的異常現象。因此必須將表格中的部分屬性,通常為產生異常現象的屬性,從原表格中分離出來形成新的表格,這種過程稱為正規化(Normalization)。正規化的過程可以使設計不好的資料庫,不再會產生異常現象。
正規化的方式即是將關聯表中所有的屬性,依其功能相依性(Functional Dependence)
分解成數個屬性子集合,然後再依每一個屬性子集合產生一個新的關聯表。也就是正規化將資料屬性組合成為一群具備良好結構的關聯表的過程。
假如舊關聯表中之所有的功能相依性都可以由分解後所產生的新關聯表中,不多不少的保留著,這種分解稱為無損分解(Lossless
Decomposition);反之則稱為有損分解。記住,並不是所有的分解都是無損分解,我們將於後面章節中介紹。
因為正規化的分解中有上述無損分解與有損分解,所以為了得到無損分解,可依下面兩個原則來做,這是由 J. Rissanen 於 1977
年所提出的:
 |
每一個原關聯表 R
中的功能相依性,在分解為 R1 與 R2 後,都要能由 R1 與 R2 中推導出。 |
 |
R1 與 R2
中的共同屬性至少是 R1 或 R2 的候選鍵。 |
|
|
|
|
 |
|
|
定義:一個關聯表為第一正規化表格,若且唯若關聯表中的每一個屬性其值皆為單值(Atomic Value)。
就資料模式而言,1NF
代表個體-關係圖轉換成的關聯表中,所有屬性都只有一個值。而之前我們曾提及,若個體-關係圖中的多值特性,我們將會另外建立一個關聯表來表示。換言之,由個體-關係圖所轉換成的關聯表已是
1NF 了,因為屬性中都只有一個值 (單值)。
|
 |
|
|
定義:一個關聯表為第二正規化表格,若且唯若關聯表中,所有非鍵值屬性完全功能相依於主鍵或候選鍵。
|
 |
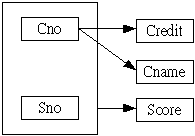
前面的學生選課資料表格
SC,其功能相依性如下: |
| |
|
(Sno,
Cno) → Score
Cno
→ Cname
Cno
→ Credit
|
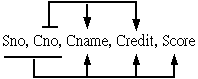
|
|
| |
而功能相依圖如下: |
| |
 |
| |
由前面的分析,我們知道它會造成新增、刪除與更新的異常,因此我們必須將其正規化,因為屬性 Credit 與 Cname
並非完全功能相依於主鍵(Sno, Cno),所以可利用 Rissanen 的原則,加以分解為兩個關聯表 R1(Sno, Cno,
Score) 與 R2(Cno, Cname, Credit):
R1 的功能相依性(FD) 如下:
(Sno, Cno)→Score
R2 的功能相依性(FD) 如下:
Cno→ Cname, Credit
R1(Sno, Cno, Score):
R2(Cno, Cname, Credit): |
| |
|
Sno
|
Cno
|
Score
|
|
Cno
|
Cname
|
Credit
|
|
S1879032
|
Math1416
|
60
|
|
Math1416
|
工程數學(一)
|
3
|
|
S1879044
|
Math1416
|
80
|
|
Cs1318
|
計算機概論
|
4
|
|
S1882032
|
Cs1318
|
58
|
|
…
|
…
|
…
|
|
S1882044
|
Cs1318
|
80
|
|
Cs1446
|
資料庫
|
2
|
|
…
|
…
|
…
|
|
|
|
|
|
S1879032
|
Cs1446
|
65
|
|
|
|
|
|
| |
若我們仔細注意分解後的兩個關聯表,我們會發現原關聯表 R 中的功能相依性的決定者(Cno) 在 R2 中為主鍵,而在 R1
中則成為了外來鍵。如此一來,原關聯表 R 中的所有功能相依性仍能保留著。而且 R1 與 R2
都不存在部份功能相依性,所以都是第二正規化表格,我們並且可以檢視原來在R中的新增、刪除與更新異常現象在R1 與
R2都沒有出現,因此達成了正規化的目的。
|
|
 |
|
|
定義:一個關聯表為第三正規化表格,若且唯若:
1. 該關聯表為第二正規化表格
(也就是關聯表中的非鍵值屬性完全功能相依於主鍵或候選鍵)。
2. 該關聯表中非鍵值屬性間,不存在遞移相依性
(也就是非鍵值屬性間,不存在著功能相依性)。
|
 |
課程資料表格
Course,其中包括課程代碼(Cno)、課程名稱(Cname)、授課教師代碼(Tno) 與授課教師名字(Tname),而課程代碼(Cno)
為主鍵。
|
| |
|
Cno
|
Cname
|
Tno
|
Tname
|
|
Cs1413
|
計概
|
C4312
|
林大為
|
|
Cs1463
|
資料庫
|
C5632
|
張小興
|
|
Cs2534
|
網路管理
|
C4312
|
林大為
|
|
…
|
…
|
…
|
…
|
|
Mis4618
|
生產管理
|
M6468
|
陳一山
|
|
Cs4341
|
專家系統
|
C5632
|
張小興
|
|
| |
其功能相依性(FD) 如下:
|
| |
|
Cno→Cname, Tno, Tname
Tno→Tname
|
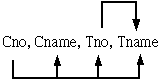
|
|
| |
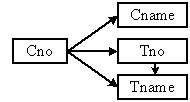
其功能相依圖如下: |
| |
 |
| |
我們可檢視其功能相依性,可得知關聯表 Course 並沒有存在非鍵值屬性部份功能相依於鍵值屬性,因此關聯表 Course
為第二正規化表格。但是,我們必須檢視其是否仍存在新增、刪除與更新的異常現象:
|
| |
(1)
假設學校新聘了個新老師黃小鵬,其教師代碼(Tno) 為 C8688,但他未開任何課程所以也就沒有課程代碼(Cno) 與課程名稱(Cname),因此
Cno 與 Cname 為虛值(Null)。如果我們欲將這些資料新增到表格 Course 中
|
| |
|
| |
便會使得主鍵 Cno 為虛值(Null),如此違反了關聯式資料模式的個體整合限制規則(Entity Integrity
Rules) 中的主鍵不可為虛值的規定。這種因新增資料而產生的異常現象,稱為新增異常。
|
| |
(2)
假設陳一山老師這學期只開一門生產管理課程,而後因人數不足而沒開成,因此必須將這筆記錄刪除
|
| |
|
| |
由於原先陳一山老師只開一門課,所以資料表格中,只有一筆陳一山老師的資料,因此刪除這記錄時,會造成陳一山老師的資料例如名字與教師代碼也一併被刪除,因而造成資料的遺失,這種因刪除時,刪除了有用資料的情況,稱為刪除異常。
|
| |
(3)
假設林大為老師因為個人因素改名為林大偉,因此必須重覆修改資料庫表個中其教師名字。萬一不小心只修改了部份的教師名字時,便會造成資料的不一致的情況。這種因資料的重覆,因而在修改時必須更改多筆記錄,否則會造成不一致的情況,稱為更新異常。
|
| |
根據第二正規化的定義,關聯表
Course
為第二正規化表格,但是仍然存在著新增、刪除與更新等異常現象,其主要的問題是因為非鍵值間存在的功能相依性,也就是遞移相依性:Tno→Tname。於是我們依
Rissan 的分解原則將 Tno→Tname 由原來表格 Course 中分解出,而形成二個關聯表 Course1 (Cno,
Cname, Tno) 與 Teacher(Tno, Tname):
|
| |
表格 Course1
的功能相依性(FD) 如下:
Cno→Cname, Tno
表格 Teacher 的功能相依性如下:
Tno→Tname
|
| |
Course1 (Cno, Cname, Tno):
Teacher(Tno, Tname): |
| |
|
Cno
|
Cname
|
Tno
|
|
Tno
|
Tname
|
|
Cs1413
|
計概
|
C4312
|
|
C4312
|
林大為
|
|
Cs1463
|
資料庫
|
C5632
|
|
C5632
|
張小興
|
|
…
|
…
|
…
|
|
…
|
…
|
|
Cs2534
|
網路管理
|
C4312
|
|
M6468
|
陳一山
|
|
Mis4618
|
生產管理
|
M6468
|
|
|
|
|
Cs4341
|
專家系統
|
C5632
|
|
|
|
|
| |
若我們仔細注意分解後的兩個關聯表,我們會發現原關聯表 Course 中的功能相依性之決定者(Tno) 在 Teacher
表格中成為了主鍵,而在 Course1 表格中則成為了外來鍵。如此原關聯表 Course
的所有的功能相依性都能全部保留。而且表格 Course1 與 Teacher
都不存在遞移相依性,所以都是第三正規化表格,我們並且可以檢視原來在R中的新增、刪除與更新異常現象在Course1 與
Teacher 沒有出現,因此達成了正規化的目的。 |
|
| |

