| |
|
 |
|
|
當我們設計資料庫中的關聯式綱要時,如何表現出屬性間的關係是一件非常重要的工作,這些屬性間的關係就是所謂的功能相依性(Functional
Dependencies)。
|
|
 功能相依性(Functional Dependency,FD)
功能相依性(Functional Dependency,FD) |
|
定義:假如 R 代表一個關聯表,X 與 Y 為 R
的屬性的子集合。若且唯若(If and only if) R 的 X 值可以唯一決定 Y 的值時,稱為“Y
功能相依於 X”(Y is functionally Dependent on X) 或稱為“X
功能決定 Y”(X funtionally determines Y),以 X→Y 表示。換另一種說法:若且唯若對於 R 中的每一個 X
值,都有唯一的 Y 值與其對應。
|
 |
學生選課資料中包括學生學號(Sno)、課程代號(Cno)、學分數(Credit)
與成績(Score)。其功能相依性 FD 如下:
(Sno , Cno) → Score,Cno →Cname ,Cno → Credit
其中(Sno , Cno) 為主鍵,它可決定唯一的 Credit 值與 Score 值。
|
| |
|
Sno
|
Cno
|
Cname
|
Credit
|
Score
|
|
S1879032
|
Math1416
|
工程數學(一)
|
3
|
60
|
|
S1879044
|
Math1416
|
工程數學(一)
|
3
|
80
|
|
S1879044
|
Cs1318
|
計算機概論
|
4
|
80
|
|
…
|
…
|
…
|
…
|
…
|
|
S1879032
|
Cs1446
|
資料庫
|
2
|
65
|
圖 1 學生選課表格 SC
|
|
 |
|
|
若 X→Y 時,X 稱為功能相依決定者(determinant),Y
則稱為功能相依者(Dependent)。
值得注意的是,如果 X 是關聯表 R 中的候選鍵 (或是主鍵),則 R 中所有的屬性必須功能相依於 X。如例 1
中,所有的屬性都功能相依於主鍵(Sno , Cno)。
|
(Armstrong's Axioms) |
|
|
功能相依性必須依循阿姆斯壯定理,這些定理可以用來對功能相依性做進一步的處理,其主要目的在於推導隱含(Implicit) 的功能相依性集合。
假設 A、B、C、D 為關聯表 R 的屬性中的三個任意子集合(Subset),而且 AB 表示 A 聯集 B。則阿姆斯壯定理如下:
|
 |
反身性(Reflexivity):若 B 是 A
的子集合,則 A→B。 |
 |
擴增性(Augmentation):若 A→B,則
AC→BC。 |
 |
遞移性(Transitivity):若 A→B,且
B→C 則 A→C。 |
|
|
以上三個定理可利用功能相依性的基本定義來證明,稱為基本定理。
|
 |
分解性(Decomposition):若 A→BC
則 A→B 且 A→C。 |
 |
聯合性(Union):若 A→B 且 A→C 則
A→BC。 |
 |
虛擬遞移性(Pseudotransitive):若
A→B 且 BC→D 則 AC→D。 |
|
|
以上的定理,可利用阿姆斯壯定理的基本定理證明,稱為衍生定理。
阿姆斯壯定理可利用已知的功能相依性,推導出其他隱含(Implicit) 的功能相依性,這些定理在於找出關聯表中的候選鍵或主鍵是相當有用的工具。
|
 |
|
|
功能相依性(FD)
集合可以用圖的方式表示,稱為功能相依圖(Functional Dependency Diagram,
FD Diagram)。
|
 |
學生選課資料的功能相依性(FD)
為:
|
(Sno,
Cno) → Score
Cno
→ Cname
Cno
→ Credit
|
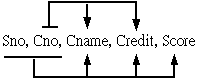
|
其功能相依圖如下: |
| |
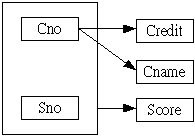
圖 1 學生選課資料的功能相依圖
|
|
| |

