下面只討論強迫振動的部分，為此引入頻率比(Frequency ratio)及靜力偏移(Statical

deflection)兩個參數：

                                                                                    (1)

                                                                                               (2)

        則方程(1)和(2)可寫成

                                                                                    (3)

                                                                                                (4)

工程中常用放大因子(Magnification Factor)來表示強迫振動的振幅與靜力偏移

的比值。由(3)式得

                                                     (5)

方程(5)為無因次式。寫成無因次式的好處不只在於它所表示的各物理量之間的數量關係

與所選用的單位無關，更重要的是他揭示了強迫振動的振幅只決定於三個因素：靜力偏

移、阻尼比、和頻率比。在低阻尼情形下，這三個因素中，頻率比對振幅的影

響最為重要。許多工程問題中，最關心的問題是放大因子如何隨頻率比而變化。

圖1畫出了放大因子隨頻率比變化的一族曲線，圖中橫座標為，縱座標為

，作為參數。這樣的曲線稱為幅頻響應曲線(Frequency response curve)，這是振動

理論中最重要的曲線之一。

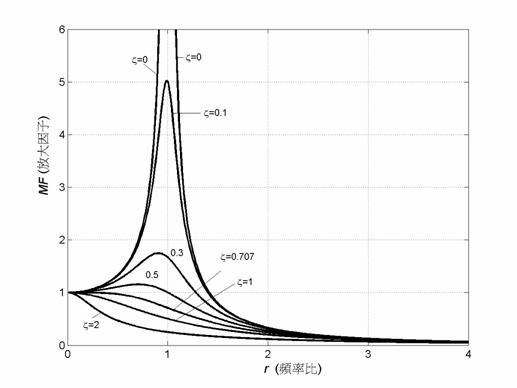
                                       圖1 簡諧激振之幅頻響應曲線

下面討論曲線變化情形

(1)低頻區

當外加激振力的頻率很低時，頻率比很小，。由(5)式不難看出，式中分母

接近於1，於是。這表示強迫振動的振幅接近於靜力偏移。此時

外加激振力的作用接近於靜力作用，系統的外激振力主要由彈簧力來平衡。從圖中

可看出，當時，如阻尼比，則阻尼對的影響很小，可略去

不計。

(2)共振區

實際上最關心的問題是：在什麼情況下達到最大值，因為這表示振幅最大。為

了求的最大值，令，由(5)式可證明在的條件下，

當時，為最大值：

                                                                                       (6)

在許多實際問題中，很小，，故可近似地當作時，達到最大值，並可

近似地表示為

                                                                                                 (7)

這說明當外加激振力的頻率接近於系統的自然頻率時，強迫振動的振幅達到最大值，這

種現象稱為共振(Resonance)。通常以為共振區，此時系統的慣性力與彈簧

力相互平衡；激振力與阻尼力相互平衡。

(3)高頻區

當外加激振力的頻率很高時，。由(1-6.18)式可知，分母增大，的值變

小，系統的外激振力主要由慣性力來平衡，且的值隨的增加而趨近於零。這

說明對自然頻率很低的系統，在高頻外力作用下幾乎沒有響應。

應注意，以上討論的隨的變化規律都是對低阻尼情形而言。如果阻尼相

當大，時，幅頻響應曲線不會出現上面三個不同區域的特徵，

從開始1單調下降趨近於零。因此，在時不會出現共振。

實際上，除了振幅外，我們還常常關心強迫振動與激振力之間的相位差如何隨

而變化。圖2畫出隨而變化的曲線，橫座標為，縱座標為，而阻尼比作為

參數。這種曲線稱為相頻響應曲線(Phase response curve)。由圖可見，相位差總在

到之間變化。在低頻區，，。在共振區，，。這說明在

共振時，系統強迫振動的相位角比激振力的相位角落後。在高頻區，，

。這表明當激振力的頻率遠高於系統的自然頻率時，強迫振動的位移和激振

力反相。

圖2 簡諧激振之相頻響應曲線